三相异步电动机空载电流的经验计算公式

三相异步电动机空载运行时，定子三相绕组中通过的电流，称为空载电流。绝大部分的空载电流用来产生旋转磁场，称为空载激磁电流，是空载电流的无功分量。还有很小一部分空载电流用于产生电动机空载运行时的各种功率损耗（如摩擦、通风和铁芯损耗等），这一部分是空载电流的有功分量，因占的比例很小，可忽略不计。因此，空载电流可以认为都是无功电流。从这一观点来看，它越小越好，这样电动机的功率因数提高了，对电网供电是有好处的。如果空载电流大，因定子绕组的导线截面积是一定的，允许通过的电流是一定的，则允许流过导线的有功电流就只能减小，电动机所能带动的负载就要减小，电动机出力降低，带过大的负载时，绕组就容易发热。但是，空载电流也不能过小，否则又要影响到电动机的其他性能。总之，空载电流是三相异步电动机的重要参数，它是鉴定电动机制造和修理质量的重要标准之一。在电动机的修理工作中，往往需要知道电动机损坏前的空载电流值，以便与修复后的空载电流值进行比较，从而判断修理质量好坏。但是，在电动机的铭牌或产品说明书上，一般不标注空载电流的额定数据，如果运行时没有留下空载电流数据，只可用计算方法来确定电动机的空载电流值。

（1） 根据电动机的简化原理图推导出来的计算公式如下：

=mcos           (3-19)

m=tg-

sin=

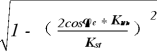
式中 ——电动机的空载电流，A；

——电动机的额定电流，A；

cos——额定功率因数；

——额定功率因数角；

——起动功率因数角；

tg——对应于角的正切；

tg——对应于角的正切；

sin——对应于角的正弦；

——起动电流倍数，即起动电流与额定电流之比；

——起动转矩倍数，即起动转矩与额定转矩之比。

此公式计算所需用的原始参数（产品目录的数据）太多，且不易获得；再就是计算麻烦、费时。所以，它在理论上讲是正确的。但在实用计算上很不方便，故不多述。

（2） 对大量试验数据的分析和统计，归纳出的实用近似公式：

=K[(1-cos)]       (3-20)

式中 ——电动机的额定电流，A，由铭牌上查得；

cos——额定功率因数，由铭牌上查得；

K——计算用系数，查看表3-2可得。

表3-2    K与cos和极数的关系

此实用近似公式简单，计算所需用的参数可由电动机的铭牌查出。但在运用公式计算时要注意：计算用系数K值的选择既受功率因数的控制，又受电动机极数的控制，因而使用也有些不方便。另外当从一个区间向另一个区间过渡时，K值发生突变。由于与K成正比，因而发生突变，可能造成较大的误差。

（3） 从实践中得出的经验公式如下：

=(2.26-K)             (3-21)

式中——电动机定子额定电流，A，由铭牌上查出；

——额定功率因数，由铭牌查出；

K——计算用系数，当≤0.85时，K=2.1；当>0.85时，K=2.15.

此经验公式比公式（3-20）更简单，没有开方和平方运算。

【例1】   一台J-61-4型三相异步电动机的铭牌数据为=13KW;=380V，=25.5A，=0.88，试确定该电动机的空载电流值。

解（1）用公式（3-20）计算。

因=0.88>0.85，且电动机为4极，查表3-2得K=5.5.将已知数据代入式（3-20）得：

=5.5[(1-0.88)×]×25.5=8.08(A)

(2)用公式（3-21）计算。

因=0.88>0.85，故K=2.15.将已知数据代入式（3-21）得：

=25.5×0.88×(2.26-2.15×0.88)=8.3(A)

该电动机的实测值为=8.15A，所以公式（3-20）和（3-21）的计算值与实测值很接近。

【例2】   一台Y180M-6型Y系列三相异步电动机的铭牌数据为=15KW，=380V,=32A，=0.81，=0.88，试确定该电动机的空载电流值。

解 （1）用公式（3-20）计算。

因=0.81，且电动机为6极，查表3-2得K=4.2.将已知数据代入式（3-20）得：

=4.2×[(1-0.81)×]×32=14.8(A)

(2)用公式（3-21）计算。

因=0.81<0.85，故K=2.1.将已知数据代入式（3-21）得：

=32×0.81×(2.26-2.1×0.81)=14.5(A)

该电动机在投入运行前曾实测，得=14.4A。